How to Calculate Percentile Using Z-Score: A Step-by-Step Guide with Examples

In statistical analysis, percentiles are crucial indicators for determining the relative position of data points within a dataset. This guide provides a systematic explanation of calculating percentiles using Z-scores, along with practical tool recommendations.

1、Core Concepts and Formulas.

1.1 Definition of Percentile

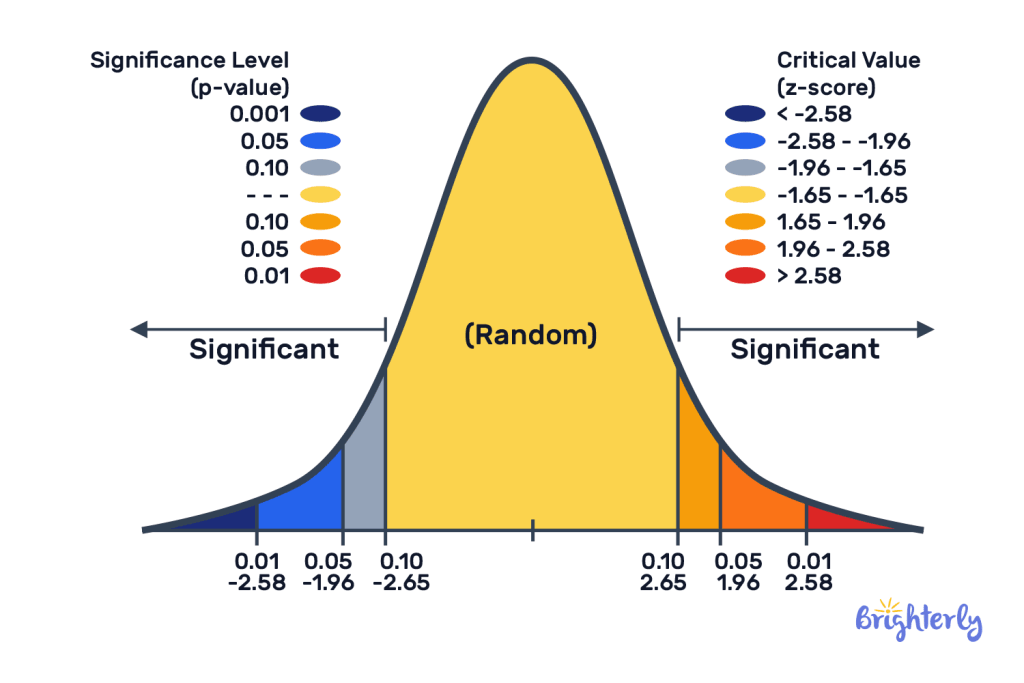
A percentile divides a dataset into 100 equal parts, where the p-th percentile indicates that p% of data points are less than or equal to this value. Key examples:

★50th percentile = Median

★75th percentile = Upper quartile

1.2 Z Score Formula

Calculation formula:

\(Z = \frac{X - \mu}{\sigma}\)

Where:

★X: Raw score

★\(\mu\): Mean of the dataset

★\(\sigma\): Standard deviation

This standardization process eliminates scale differences between datasets.

2、Step-by-Step Calculation Process

2.1 Calculate Z-Score

★Compute dataset mean \(\mu\) and standard deviation \(\sigma\)

★Apply the Z score formula

★Use Z-Score Calculator

2.2 Convert to Cumulative Probability

Three methods:

★Z score table lookup

★Excel function: =NORM.S.DIST(z, TRUE)

★Online tool: P value Calculator

2.3 Determine Percentile

Conversion formula:

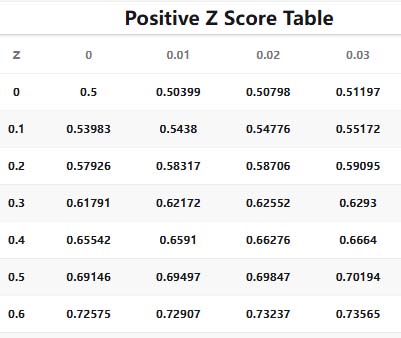
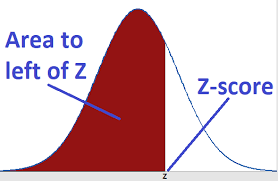
Percentile = P(Z ≤ z) × 100

Example calculation (Z = 1.28):

★Cumulative probability: 0.8997

★0.8997×100=89.970.8997×100=89.97

★Rounded to 90th percentile

3、Z-Score to Percentile Conversion Table (Extended with Integer Percentiles)

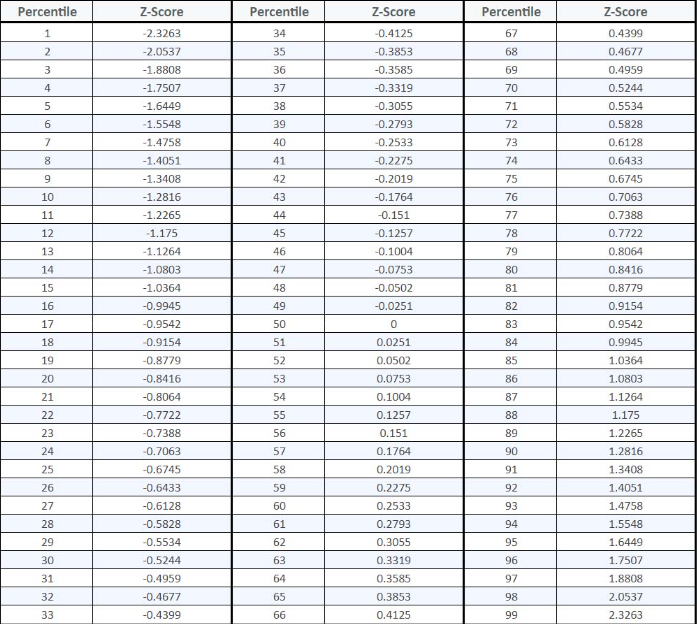
For practical applications, here's an enhanced reference table showing both common Z-scores and their corresponding integer percentiles