Complete Guide to Z Score: From Formula Analysis to Business Applications (Essential Statistical Tool for Data Analysts)

1、The Essence of Z-Score: A GPS Positioning System in the Data World

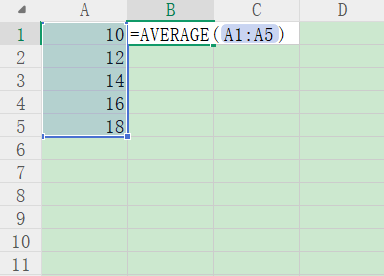
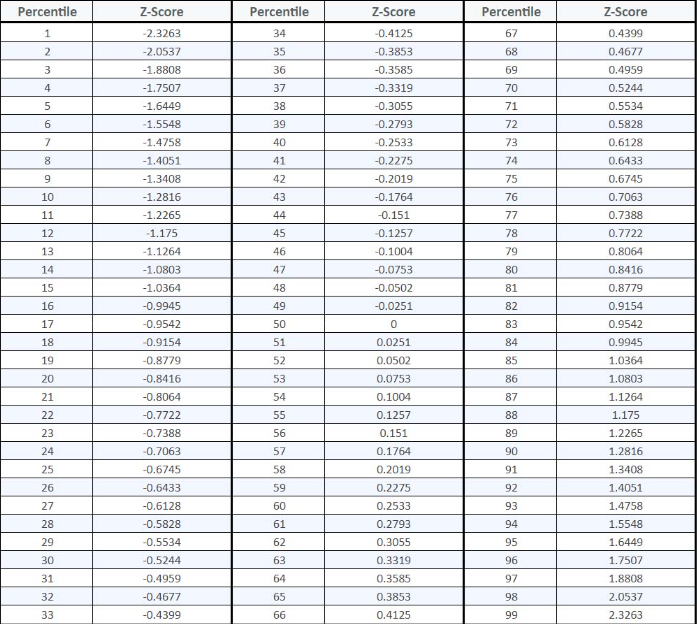
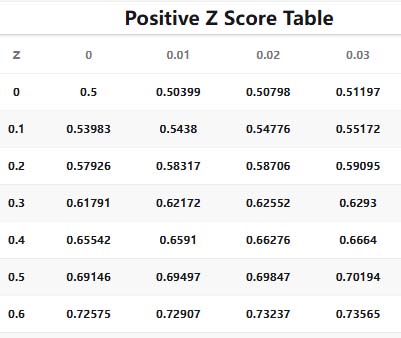
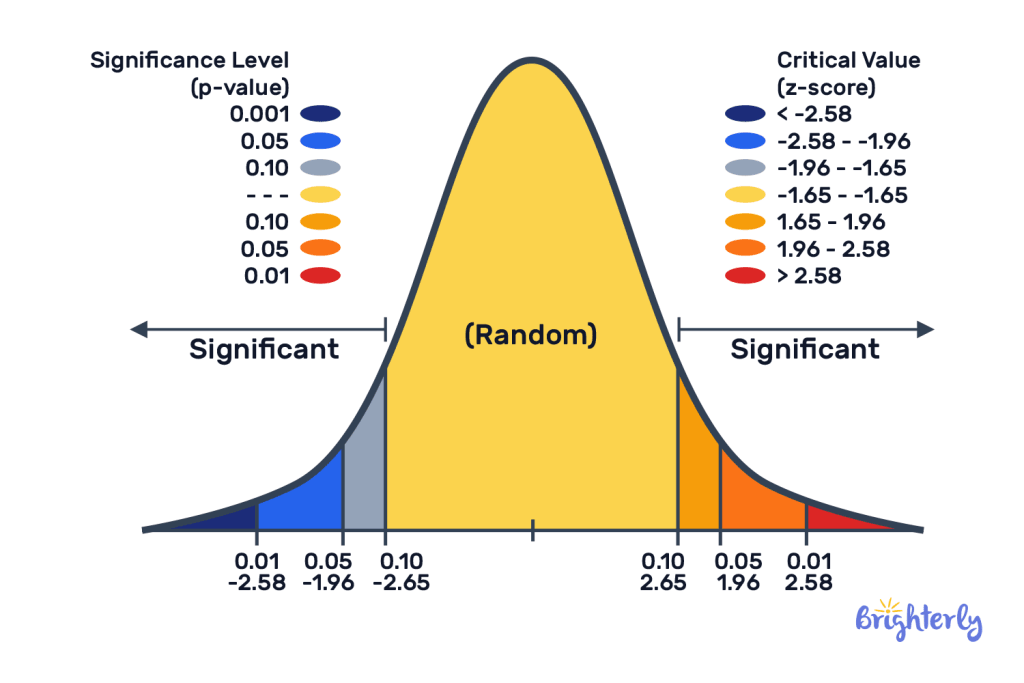
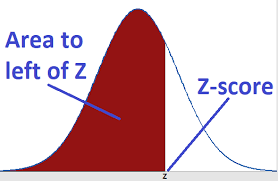
The Z-score (standard score/Z value) is a core statistical metric for quantifying data's relative position. By calculating how many standard deviations a data point is from the mean, it achieves three key functions:

★Precision Positioning: Z > 0 indicates superior performance to the average, while Z < 0 signals below-benchmark results (e.g., store sales vs. regional averages)

★Cross-Dimensional Comparison: Eliminates unit differences for standardized comparisons across datasets (e.g., evaluating height and weight anomalies simultaneously)

★Risk Alert: Widely used in finance for bankruptcy prediction (Altman Z-score model application)

2、Deep Dive into Z-Score Formulas (With Industry Use Cases)

2.1 Single Data Point Formula: \(Z = \frac{X - \mu}{\sigma}\)

Parameter Interpretation:

★X: Business metric (daily foot traffic/single SKU inventory)

★\(\mu\): Industry benchmark (regional weekly average foot traffic/category safety stock standard)

★\(\sigma\): Market volatility coefficient (standard deviation of foot traffic/inventory turnover fluctuation)

2.2 Sample Mean Formula: \(Z = \frac{\overline X - \mu}{\frac{\sigma}{\sqrt n}}\)

Industry Applications:

★Manufacturing: Batch product quality inspection (e.g., chip yield testing)

★Tech: A/B test significance validation (page conversion rate comparison)

★Healthcare: Drug efficacy evaluation (treatment vs. control group recovery periods)

3、Z-Value Interpretation Table (Statistical Significance & Business Actions)